2022 KINSC Scientific Imaging Contest Winners Announced

Judging is based on both the quality of the image and the explanation of the underlying science. First, second, and third place winners will have their images displayed on the walls of the KINSC.

First Prize: Ethan Baker '24

Quantum dots are tiny pieces of semiconductors that can trap electrons. When we shine light at the dots, the electrons inside can only absorb and emit specific wavelengths of light because they are trapped. The exact wavelength emitted depends on the chemical properties of the dot and its size. Here, a source of UV light is shining at four vials containing quantum dots of different sizes. The dots in each vial are absorbing the UV light and re-emitting light at a different wavelength, which creates the vibrant glowing colors.

Second Prize: Julia Smeltzer '23

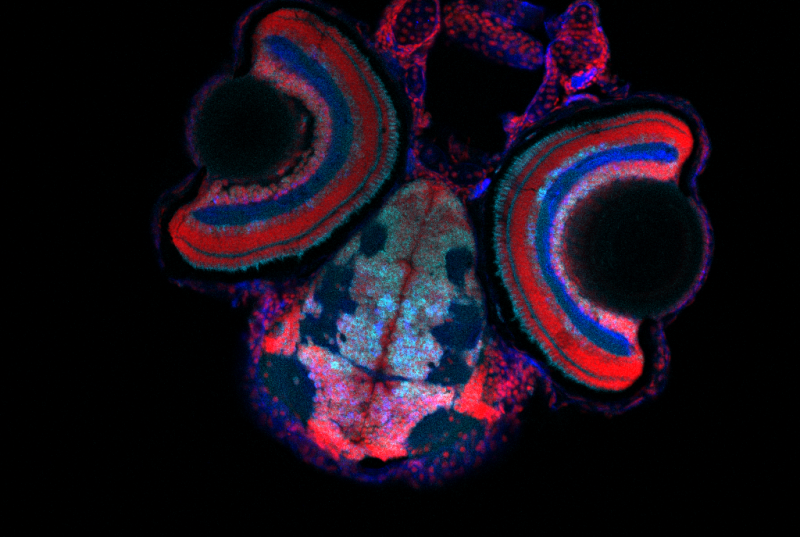
This image is a slice of a zebrafish head that was taken on the confocal microscope at a 20x objective. The image includes two zebrafish eyes as well as the zebrafish brain and mouth. Staining was done so that the ganglion cell layer and amacrine cells in the eyes could be clearly seen. This image was taken for a superlab class where we were looking at cell layers in mutant zebrafish eyes to try and understand why mutant zebrafish respond to visual stimulants differently than wild-type zebrafish. The colors were edited in FIJI image J to create this final image.

Third Prize: Woodkensia Charles '24

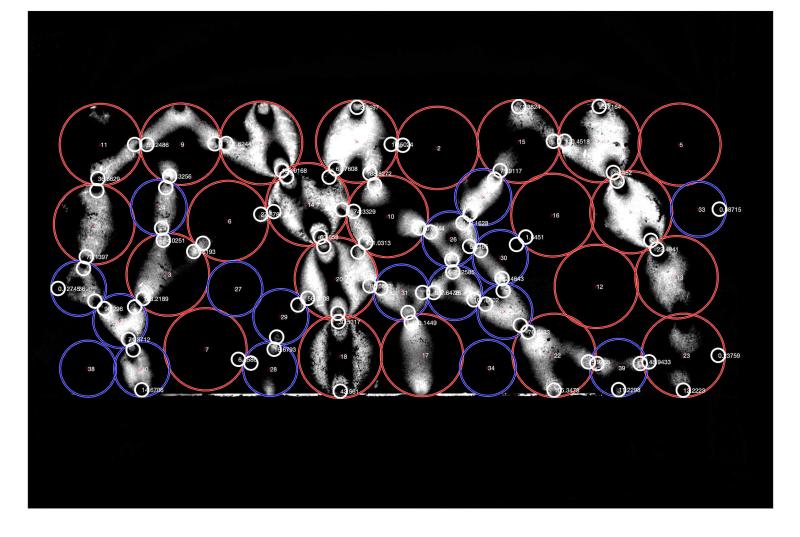
This is an image processing of a photoelastic particle in MatLab using the PEGS inversion published software. Photoelastic materials are distinctive because their birefringence is dependent on the stresses (forces experienced by an object over an area) on the material. Using polarizers, which change the polarization of light passing through them, we can take advantage of photoelasticity to visualize the stresses in a granular system. The MATLAB program identifies the locations of the particles (red and blue circles) and the contacts between them (white circles). The stress is the white skeleton figure.

Honorable Mention: James Garland '22

From dictating the lives of stars to the structure of the universe, galaxies lie at a bustling intersection of cosmic scale. Understanding how these complex and diverse systems behave can illuminate some of the most elusive problems in astrophysics. Galaxies evolve over billions of years, providing us with frozen snapshots of their lives when observed on human timescales. To supplement this, we simulate galaxies and watch them develop over time. Here, we see a telescope image and a simulated “present-day” image of two similar galaxies on the left and right. Through comparison, they mutually inform our knowledge of galaxy evolution.

Honorable Mention: Sarina Smith '23

Pictured is the fungi Hericium erinaceus (also known as lion's mane) cultured on potato dextrose agar. This mushroom is known for its culinary and medicinal uses. Research has shown that secondary metabolites produced by this fungus reduce amyloid plaque burden and other hallmarks of Alzheimer’s disease in mouse models. For my senior thesis, I plan to investigate whether these compounds can similarly inhibit or disrupt protein aggregation in other models of neurodegenerative diseases. This semester, I learned how to culture the fungus with the support of Professor Robert Fairman.

Honorable Mention: Amina Irfan BMC '25

Fractals are never-ending, infinitely-complex patterns, that are self-similar on different scales. Although fractals are very complex, they are created by repeating simple processes. Abstract fractals—such as the Mandelbrot Set—can be calculated by a computer calculating the same equation (Zn+1 = Zn2 + C ) over and over again, with different values. More complex and aesthetically pleasing images can be generated, like the Nova fractal or the Magnet fractal, by computing fractals with more complex equations over and over again!